Die Simulation zeigt dir ein Objekt, welches du als Donut kennst. Ein solcher Donut wird in der Mathematik auch als Torus bezeichnet. Auf unserem Torus sind zwei Geodäten eingezeichnet und vier Punkte markiert.
Schaue dir den Torus von allen Seiten genau an (du kannst ihn in der Simulation drehen), aktiviere gern die Hilfslinien (sie zeigen wichtige Abschnitte der Geodäten) und bearbeite anschließend die folgende Aufgabe.
Vergleiche die Geometrie der Oberfläche des Torus mit der in diesem Kurs kennengelernten Geometrien. Vervollständige anschließend folgende Aussgage:
"Die Geometrie des Torus ähnelt..."
"Ich bin dieser Meinung, da..."
"Die Geometrie des Torus ähnelt sowohl der der Kugeloberfläche als auch der der Sattelfläche. Ich bin dieser Meinung, da – je nachdem welchen Teil des Torus ich betrachte – die Geodäten parallel sein können (an je zwei markierten Punkten; die Hilfslinien zeigten dies) und sich dann entweder annähern oder von einander entfernen."
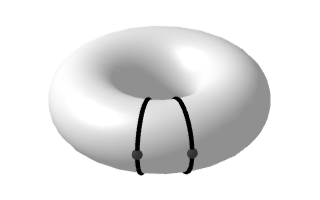

Dies zeigt, dass der Torus sowohl Eigenschaften der Kugelgeometrie als auch der Sattelgeometrie aufweist.
Es gibt also Flächen, deren geometrische Eigenschaften auch vom betrachteten Ort abhängen können.