Neben der Methode, die Fläche in Teilstücke zu zerschneiden und sie flach auf den Tisch zu drücken, kann man sie auch mit Hilfe besonderer Linien untersuchen.
Jetzt bist Du dran:
Zeichne eine Linie, die an jedem Punkt stets geradlinig verläuft.
Eine solche Linie, die an jedem Punkt stets geradlinig verläuft, bezeichnet man auch als Geodäte.
Ergänze eine zweite Geodäte, die von einem anderen Punkt aus in dieselbe Richtung startet wie die erste.
Sobald du eine zweite Geodäte gezeichnet hast, solltest du in etwa folgendes sehen:
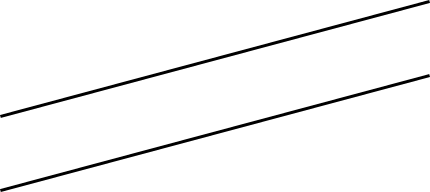
Die beiden Geodäten verlaufen in diesem Beispiel stets parallel. Ihr Abstand zueinander bleibt konstant. Auch dies ist ein Beleg dafür, dass es sich bei der Geometrie um eine euklidische Geometrie handelt.