Ausgehend von unseren Beobachtungen wollen wir die Frage "Wieso ändert das Licht seine Richtung?" beantworten.
Die parallel startenden Geodäten laufen im Außenraum um das Schwarze Loch auseinander.
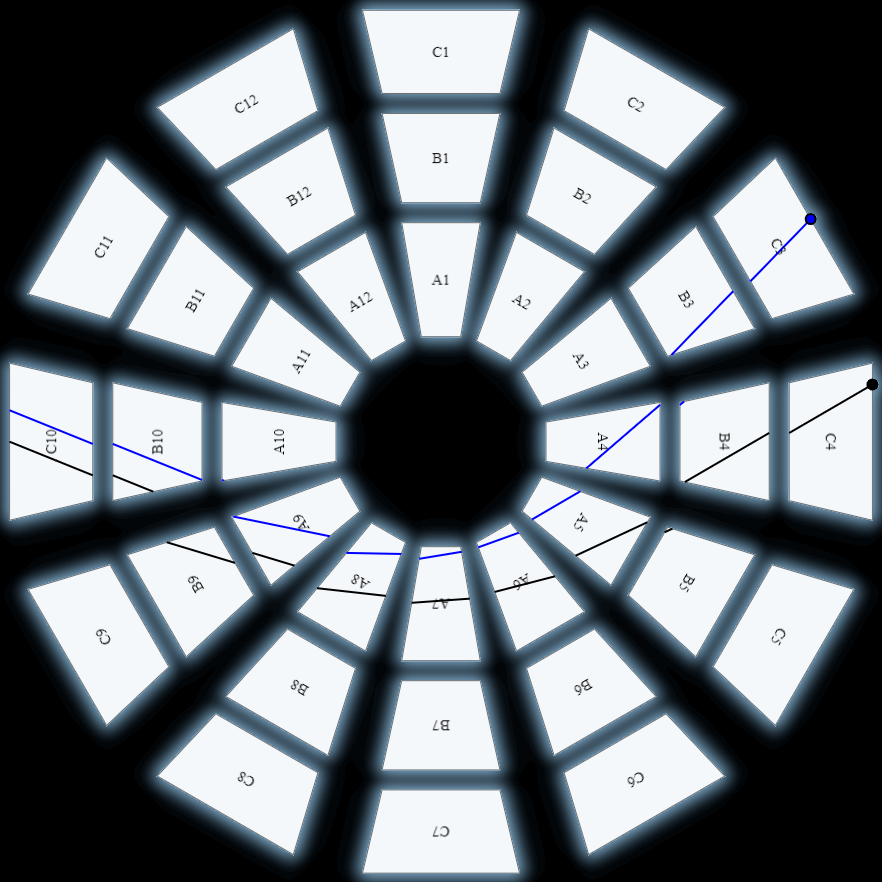
Kommt dir das bekannt vor? Richtig, in BM1 konnten wir dasselbe bei der Sattelfläche feststellen. Hier führten wir diese Beobachtungen auf die anders geartete Geometrie der Fläche zurück. Ist das hier auch so? Einstein sagt, dass massereiche Objekte die Geometrie des sie umgebenden Raumes beeinflussen. Unsere Beobachtungen bestätigen dies für den Außenraum des Schwarzen Lochs.
Doch was hat das mit Eddingtons Experiment zu tun? Hier spielt die Eigenschaft von Licht, dass es Geodäten folgt, eine zentrale Rolle. In unserem Beispiel haben wir Geodäten konstruiert, die den Bahnen von Licht sehr ähnlich sind. Wie wir feststellen konnten, verliefen unsere parallel startenden Geodäten zwar stets geradlinig über die Sektoren, zeigten jedoch später in unterschiedliche Richtungen.
Nehmen wir nun an, dass wir dies auf die Bahnen der Lichtstrahlen um die Sonne herum übertragen können, so wird deutlich, dass die Geometrie des Raumes sie beeinflusst haben muss.
Der Lichtstrahl verlief stets geradlinig, zeigte jedoch, nachdem er den Außenraum der Sonne passierte, in eine andere Richtung.
Für den Beobachter auf der Erde, in unserem Fall Eddington und sein Team, wirkt es so, als befände sich der Stern an einer anderen Position, da das Licht aus einer anderen Richtung kommt.
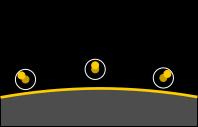
Die folgende Grafik veranschaulicht noch einmal die Entstehung von Eddingtons Beobachtung:
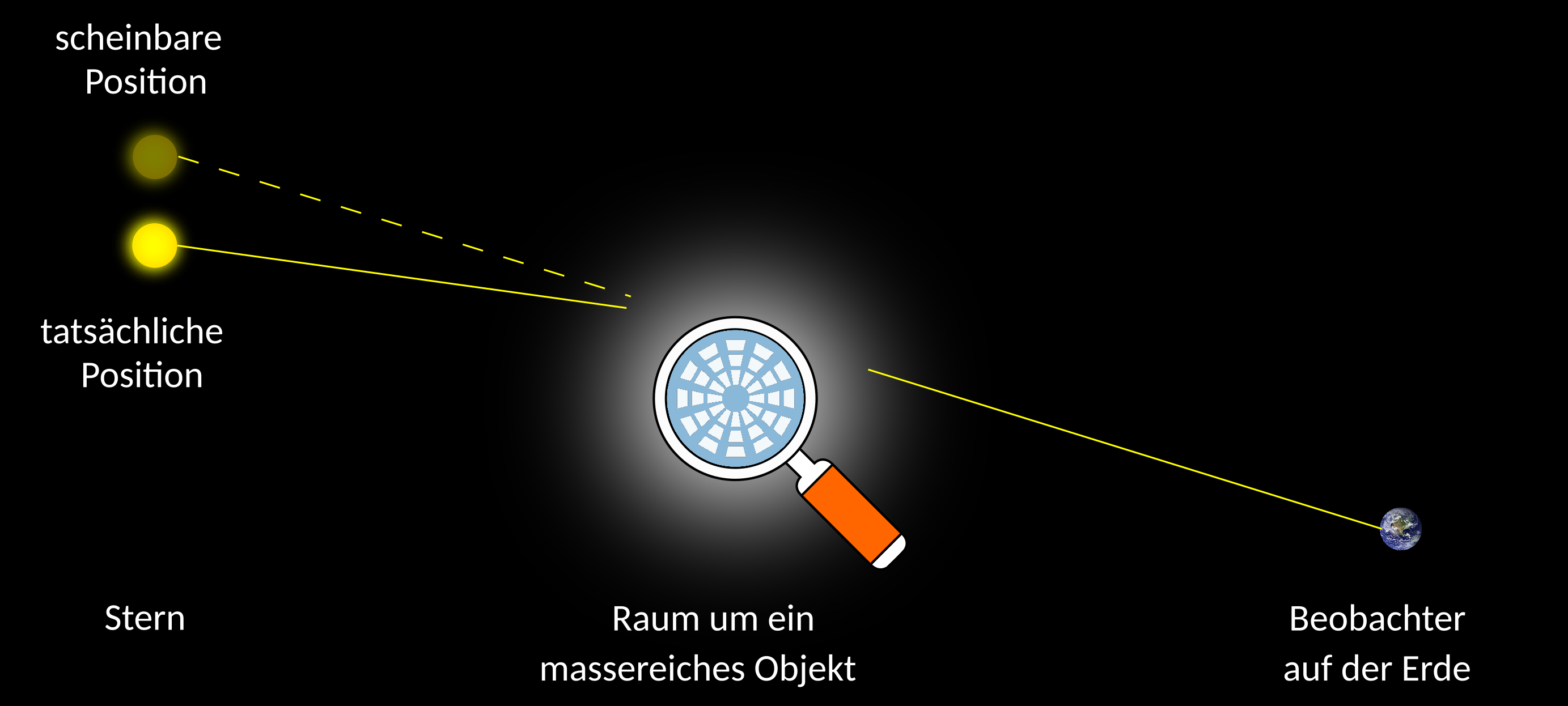
Licht breitet sich stets geradlinig aus. Wenn es einen Raum mit nicht-euklidischer Geometrie durchquert, hat es danach eine andere Richtung als vorher. Man spricht von Lichtablenkung.
Anmerkung: Mit Hilfe des Modells konstruierst du Geodäten im nicht-euklidischen Raum. Diese Geodäten sind den Bahnen von Licht sehr ähnlich. In der Realität spielt jedoch auch die Zeit eine wichtige Rolle. Wirkliche Lichtbahnen verlaufen stärker abgelenkt.